近期，清华大学高等研究院汪忠教授研究组在非厄米物理与无序系统交叉领域取得重要进展。在非厄米无序系统中，粒子可以突破波函数局域化的限制进行传播，并遵循全新的动力学标度律。他们提出了这一现象的解析理论，揭示了非厄米无序系统中一种全新的动力学标度现象：即使系统的所有本征态都呈现指数局域化（即谱局域化），波包仍能发生奇异的跳跃式传播，且其时空展宽服从由系统虚部能谱结构决定的普适标度律。这项工作澄清了非厄米局域化与经典厄米情形的关键区别，并为在开放量子体系中调控和观测反常输运现象提供了理论线索。

安德森局域化包含谱与动力学两个层面的意义：(1) 本征态局域化; (2) 扩散现象的消失。在厄米系统中，二者互为依存，本征态局域化导致扩散消失，因此这两层含义通常不作区分。然而，近年来的非厄米物理实验（如具有随机增益/损耗的光子晶格）却发现，尽管所有本征态在空间上指数局域，波包却能“逃逸”局域化的束缚，呈现出跳跃式的前进。这种“动力学退局域”现象与传统图像大不相同，但其背后是否存在普适的规律？这个问题的答案悬而未决。

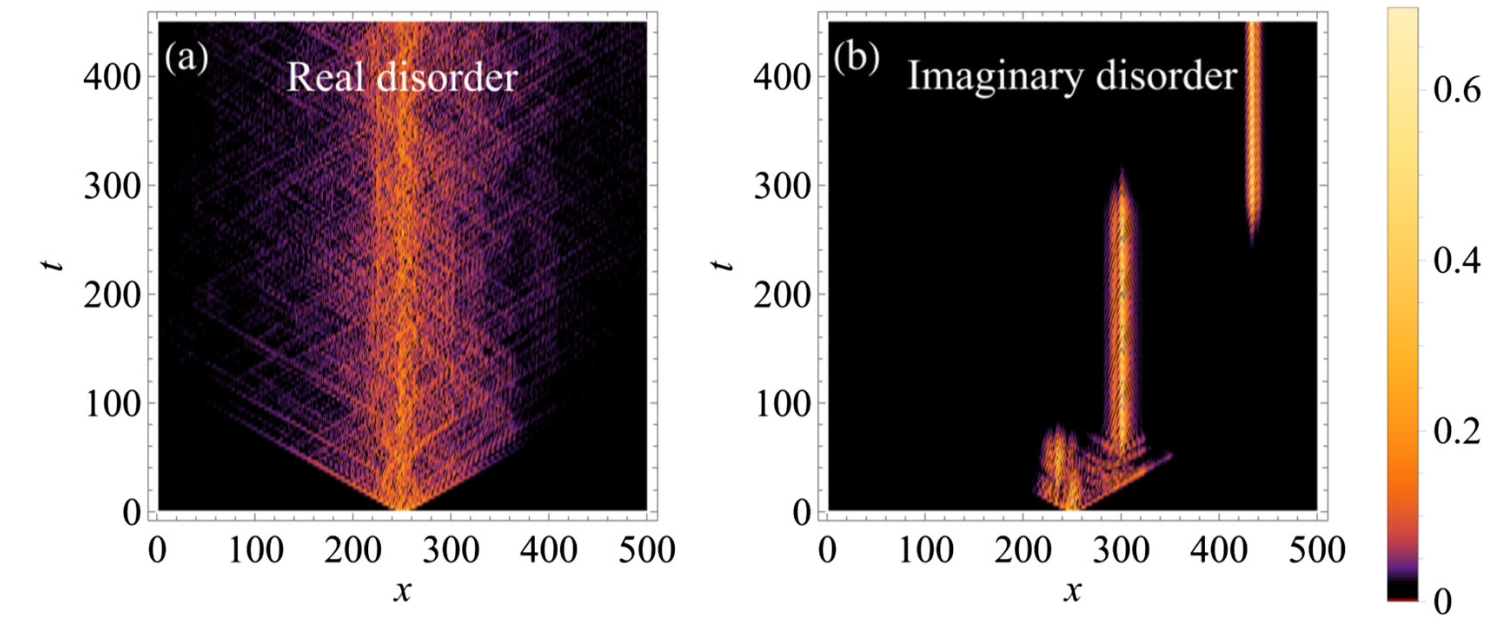
图 1 ，（a）传统无序系统中，波包只能在局域化长度内扩散。（b）非厄米无序系统中，即使本征态发生安德森局域化，波仍然可以传播。

研究团队从一个简洁的模型出发，他们考虑在纯虚数无序势中演化的波包，并将其在非厄米本征态上展开。每个本征态对波包的贡献取决于一个权重因子，该因子由两项竞争决定：一是本征态波函数随距离的指数衰减（局域化效应），二是其本征值虚部引起的指数增长（非厄米放大效应）。在任意时刻，波包的前沿位置由权重最大的本征态主导。

这个寻找最优权重因子问题的数学形式，与凝聚态物理中著名的“莫特变程跳跃” （Mott’s variable-range hopping）理论有神似之处。 在莫特的理论中，电子在局域态间的跳跃概率取决于空间距离与能量差，通过优化这两者的竞争，得到了电导率随温度变化的标度律，其中温度T的倒数（1/T）决定了能量因子的权重。而在本项研究中，时间t 扮演了与1/T非常相似的角色，它量化了能量虚部放大效应的权重。尽管两个问题的物理图景截然不同——一个是平衡态下的热激活跳跃，另一个是非平衡的量子动力学演化——但核心的优化数学结构如出一辙。这一类比为凝聚态物理与非厄米动力学的进一步交叉提供了新视角。

通过将问题转化为上述优化问题，研究团队发现，长时间后的波包展宽标度律完全由系统能量虚部态密度（ImDOS）的渐近尾部分布所主宰。基于这一核心机制，他们推导出了三类典型ImDOS对应的普适标度律：

1.高斯型分布：导致对数压低的亚弹道输运，展宽满足 |x| ∼ t / (ln t)^{1/2};

2.均匀型分布：导致维度依赖的亚扩散，|x| ∼ t^{1/(d+1)};

3.线性型尾部分布：导致另一类亚扩散，|x| ∼ t^{2/(d+2)}.

这些理论预言在一维和二维模型的数值模拟中得到了很好的验证。作者还借助重整化群理论，发现在三维空间中系统可以发生退局域化相变（delocalization transition），并且当本征态变成扩展态后，系统存在一个新的动力学标度律：|x| ∼ t^{3/5}. 这种标度律不仅超越了传统的粒子传播规律，也和上述的非厄米系统局域化态对应的规律截然不同，进一步展现出非厄米系统独特的动力学规律，有望在未来实验中得到验证。

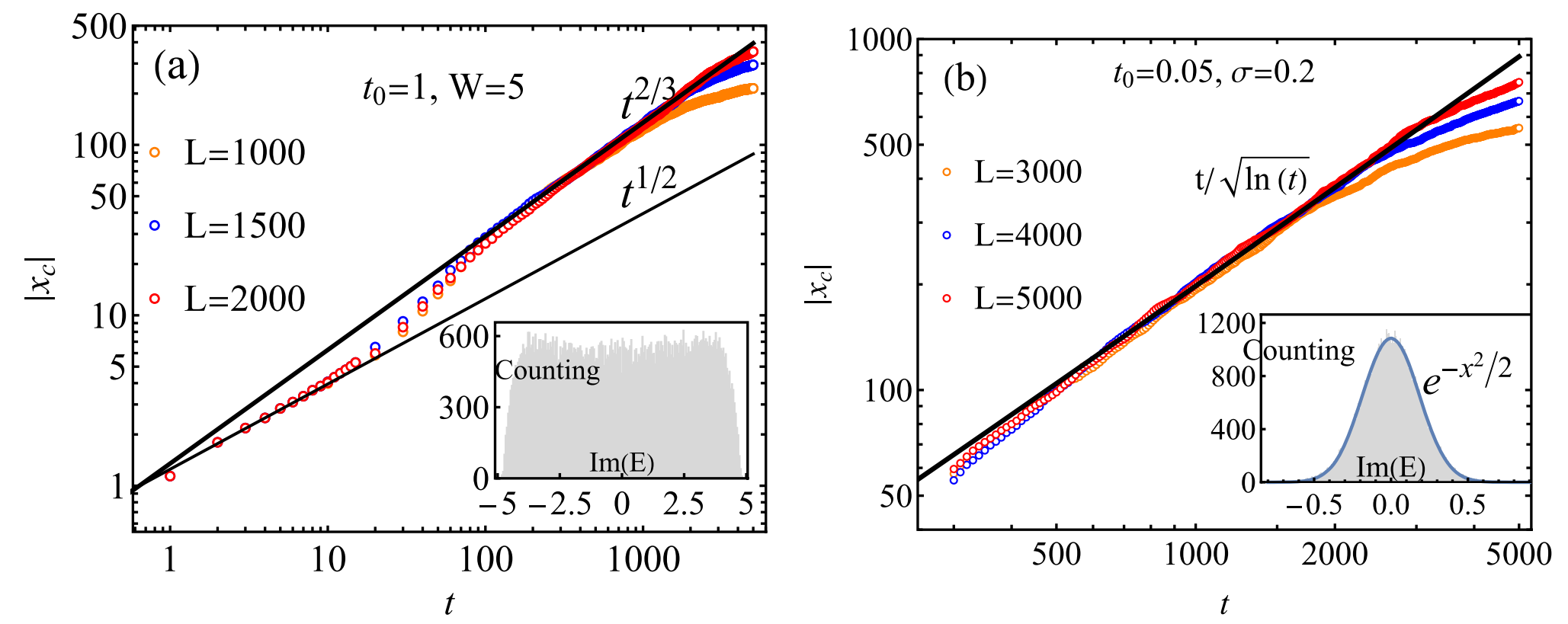
图 2 ，一维非厄米系统中粒子的传播距离与时间的关系。（a）当虚部态密度（ImDOS）整体呈现均匀分布但尾部呈现线性分布时（见插图），粒子扩散在传播早期和后期分别呈现出对应的标度律。（b）对于高斯分布型的虚部态密度，粒子传输遵循对数压低的弹道输运。

该工作的理论框架具有高度的普适性。它不仅解释了先前的光学实验观测，更可通过刘维尔动力学映射到开放量子系统。研究表明，在具有局域随机损耗的玻色腔阵列或量子行走实验中，存活粒子的空间分布将精确复现非厄米哈密顿量演化所预言的标度行为。这为在多个物理平台上（如超导量子电路、耗散光子晶格）观测和验证这一普适输运现象开辟了道路。

该研究成果以《Universal Non-Hermitian Transport in Disordered Systems》为题发表于《Physical Review Letters》。论文的第一、二作者为清华大学高等研究院博士后李博（现为西安交通大学副教授）、陈川（现为兰州大学青年研究员），通讯作者为汪忠教授。研究得到了国家自然科学基金及国家重点研发计划的资助。

论文链接：https://journals.aps.org/prl/abstract/10.1103/z9m1-3mwb