近期，清华大学高等研究院汪忠教授研究组师生在非厄米物理领域取得进展。他们提出了一种新的PT对称性（Parity-Time symmetry）破缺机制，揭示了非厄米能谱从实数向复数的转变过程与广义布里渊区（generalized Brillouin zone）的几何特征之间的密切联系，并预言了非厄米体系中一类新的能谱奇点——非布洛赫范霍夫奇点（non-Bloch van Hove singularity）。

非厄米物理是近年来一个非常活跃的研究方向。非厄米系统的一个重要特征是其能谱和波函数对边界条件异常敏感。如图1所示，在周期边界条件下，非厄米系统的本征态波函数通常是延展的布洛赫平面波；而在开放边界条件下，其本征态波函数会以指数衰减的形式局域在系统的边界，形成“趋肤模”。这一现象此前被汪忠研究组命名为非厄米趋肤效应(non-Hermitian skin effect; Yao and Wang, PRL, 121, 086803）.

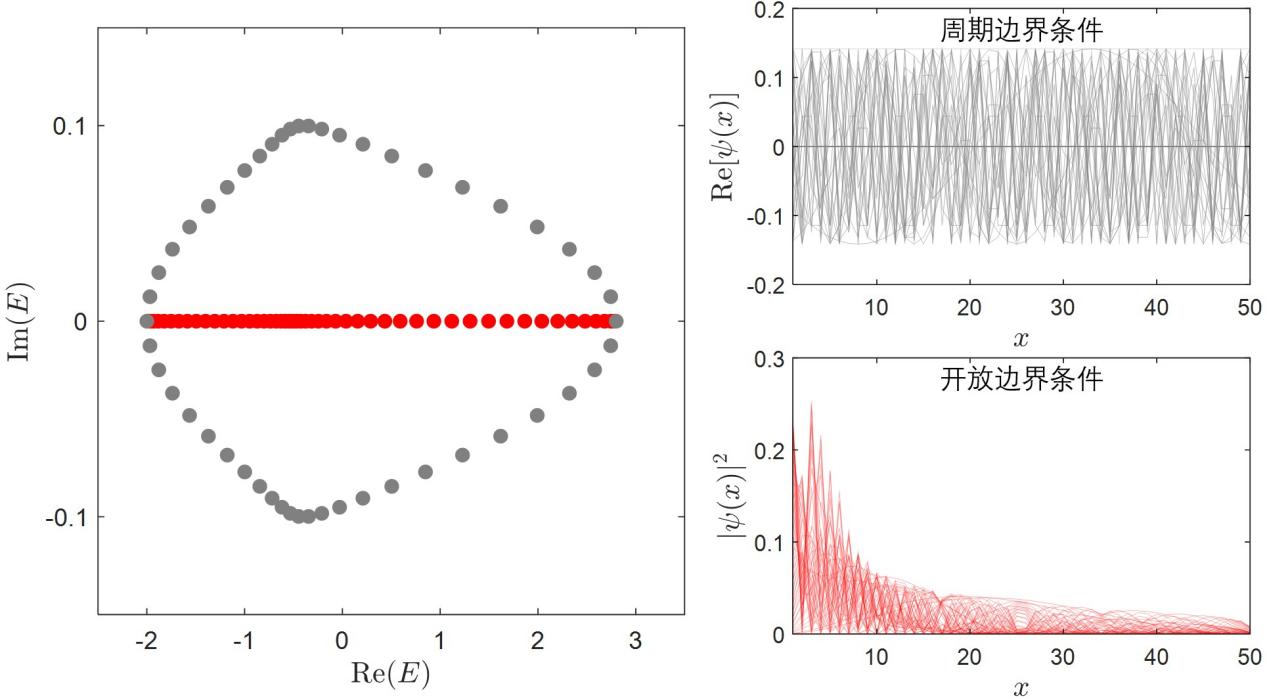
图1：左侧子图表示一个典型的非厄米系统在周期边界条件（灰色散点）和开放边界条件（红色散点）下的能谱。右上子图表示非厄米系统在周期边界条件下延展的布洛赫波函数；右下子图表示非厄米系统在开放边界条件下局域的趋肤模。

非厄米趋肤效应使得布洛赫能带理论在描述非厄米系统时不再可靠。为了刻画非厄米系统的一般物理性质，汪忠研究组此前提出了非布洛赫能带理论（non-Bloch band theory）。这一理论以广义布里渊区概念为基础，利用具有复数动量的非布洛赫波来描述本征态(趋肤模)。一个典型的广义布里渊区如图2左侧子图中的黄色曲线所示，而黑色虚线所示的单位圆则给出通常熟知的布里渊区。不难发现广义布里渊区较布里渊区有着更加丰富的几何结构，但广义布里渊区几何特征所蕴含的物理内涵并未得到充分发掘。

汪忠研究组师生的近期工作揭示了广义布里渊区几何与非厄米物理中另一个重要的物理概念宇称-时间对称性（以下简称PT对称性）之间的密切联系。PT对称性使得非厄米系统的能谱在一定条件下可以是纯实数的。在过去针对PT对称性的研究中，人们发现PT对称性的破缺，即非厄米能谱从实数到复数的转变，往往伴随着奇异点（exceptional point）的出现。当系统的参数位于奇异点时，非厄米哈密顿量的本征值和本征态均是简并的，其本征空间是不完备的。这种奇异点具有新奇的动力学和响应性质，并具有潜在应用前景。

然而，非厄米趋肤效应要求我们重新审视PT对称性及其破缺过程。过去的研究表明，具有非厄米趋肤效应的非厄米系统在周期边界条件下的能谱一定是复数(不能为纯实数)。然而，这类非厄米系统在开放边界条件下的能谱可以是纯实数的。图1左侧子图即展示了这种情况。这一现象源自于非厄米趋肤效应与PT对称性的共同作用，被称为非布洛赫PT对称性（non-Bloch PT symmetry）。在2021年，汪忠研究组与实验合作者(北京计算科学研究中心薛鹏团队以及中科大易为教授)在光子量子行走实验中观测到非布洛赫PT对称性破缺，并发现破缺过程所对应的非厄米能谱由实数到复数的转变会导致非厄米波包动力学中呈现显著的定性改变[Phys. Rev. Lett. 126, 230402 (2021)]。

尽管非布洛赫PT对称性及其对非厄米动力学的重要影响已经被实验证实，人们对非布洛赫PT对称性转变的机制仍缺乏全面的认识，仍存在一系列重要问题：非布洛赫PT对称破缺的机制是什么？如何有效预测这种破缺转变发生的参数位置？破缺转变临界点有什么普适的物理特征？汪忠师生近期的研究工作对这些问题给出了系统的回答。

图2展示了一个典型的非布洛赫PT对称性破缺过程：随着非厄米参数的变化，开放边界条件下的非厄米能谱从实数转变为复数，与此同时，广义布里渊区上将会出现若干尖点（cusp）。这些尖点如图2中蓝色散点所示。通过更加仔细的分析可以发现，在没有发生非布洛赫PT对称性破缺时，实数能谱对应的广义布里渊区是一条没有尖点的光滑闭合曲线 【图2（a,b）】；而在非布洛赫PT对称性破缺发生后，非厄米能谱在能量复平面上出现了若干分支，与之对应的广义布里渊区上出现了几何尖点【图2（e,f）】。

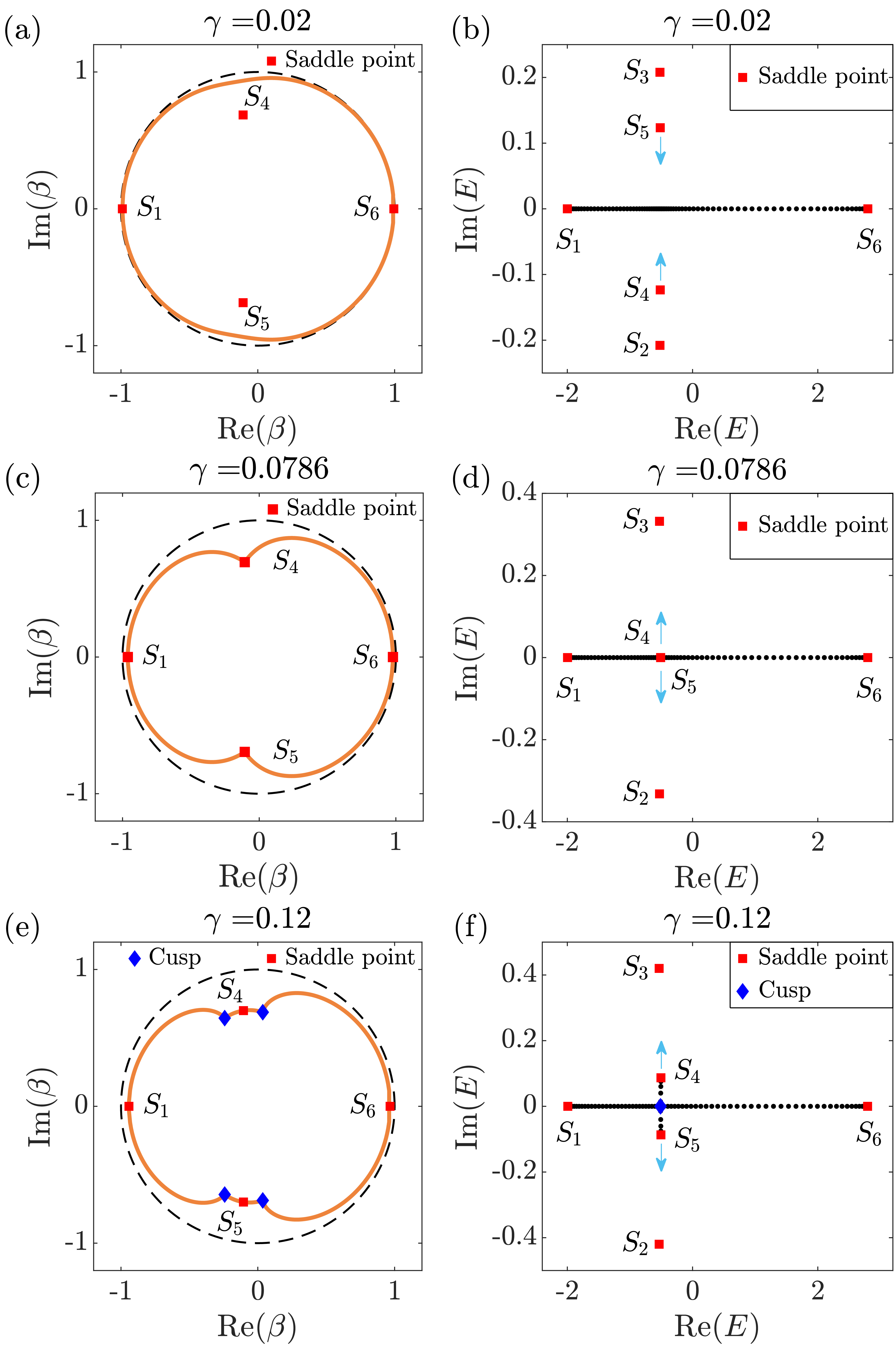
图2：左侧表示不同参数下的广义布里渊区（黄色曲线）和布里渊区（黑色虚线）；右侧表示不同参数下非厄米系统在开放边界条件下的能谱。随着非厄米参数的增大，右侧所示的开放边界条件下的非厄米能谱从实数转变为复数，左侧所示的广义布里渊区上出现尖点。

上述过程表明，广义布里渊区上尖点的出现揭示了非布洛赫PT对称性破缺的几何起源。这一基于几何尖点的破缺机制有别于传统的PT对称性破缺中基于奇异点的破缺机制，为非厄米系统PT对称性的理论和实验研究提供了新的途径。

基于这一几何图像，这项工作进一步提出了一个简洁的理论方法来判定广义布里渊区上出现尖点的条件，从而确定非布洛赫PT对称性破缺的相边界。研究发现非布洛赫PT对称性破缺的过程伴随着鞍点（saddle point）及其对应的能量在复平面上的流动，这些鞍点的分布如图2中红色散点所示。如图2（c,d）所示，当非布洛赫PT对称性破缺将要发生时，某些位于广义布里渊区外的鞍点会移动到广义布里渊区上，且这些鞍点的能量在实轴上汇合。这些鞍点的位置和鞍点能量汇合的条件可以利用系统具有的布洛赫哈密顿量，并结合代数概念“结式”（resultant）高效确定。通过鞍点重合条件确定的相变界位置与精确对角化的数值计算所得到的结果非常吻合【图3】。

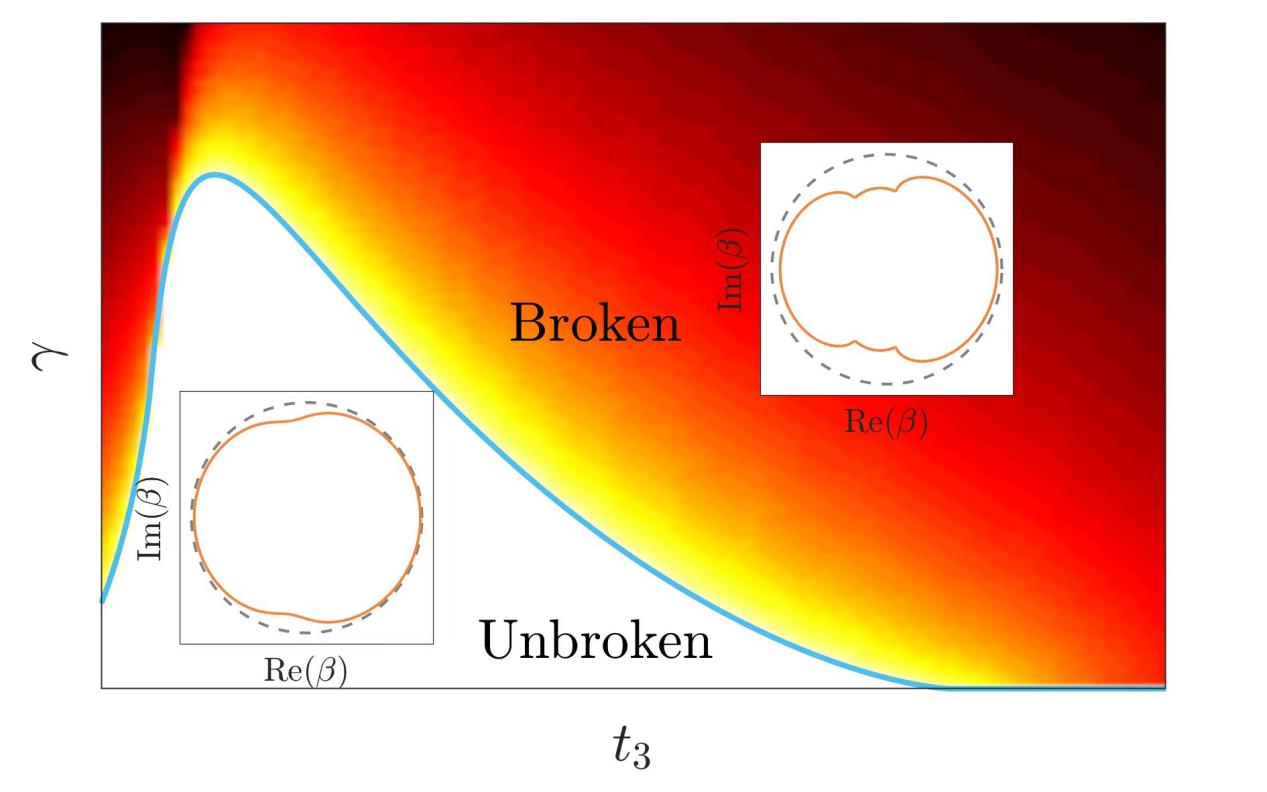
图3：基于代数方法得到的非布洛赫PT对称性破缺的相边界（蓝色曲线）与基于精确对角化的数值计算结果相符。白色区域表示没有发生非布洛赫PT对称性破缺的参数区间，彩色区域表示发生非布洛赫PT对称性破缺的参数区间。

当系统的参数取在非布洛赫PT对称性破缺的相边界时，系统在开放边界条件下的能谱依旧是纯实数，此时的广义布里渊区上恰好出现几何尖点【图2（c,d）】。在这种情况下，系统的实数能谱上会出现一类全新的能谱奇点，它有着与厄米系统中范霍夫奇点类似的能态密度（density of states）发散行为【图4】。它源自广义布里渊区上的几何尖点，因此，作者们称这类奇点为非布洛赫范霍夫奇点（non-Bloch van Hove singularity）。就像封闭多体系统中的范霍夫奇点有助于诱导出超导、电荷密度波等量子态，本研究发现的非布洛赫范霍奇点也有望在开放或非厄米量子多体系统的研究中发挥作用，为利用非布洛赫PT对称性打开新的思路。

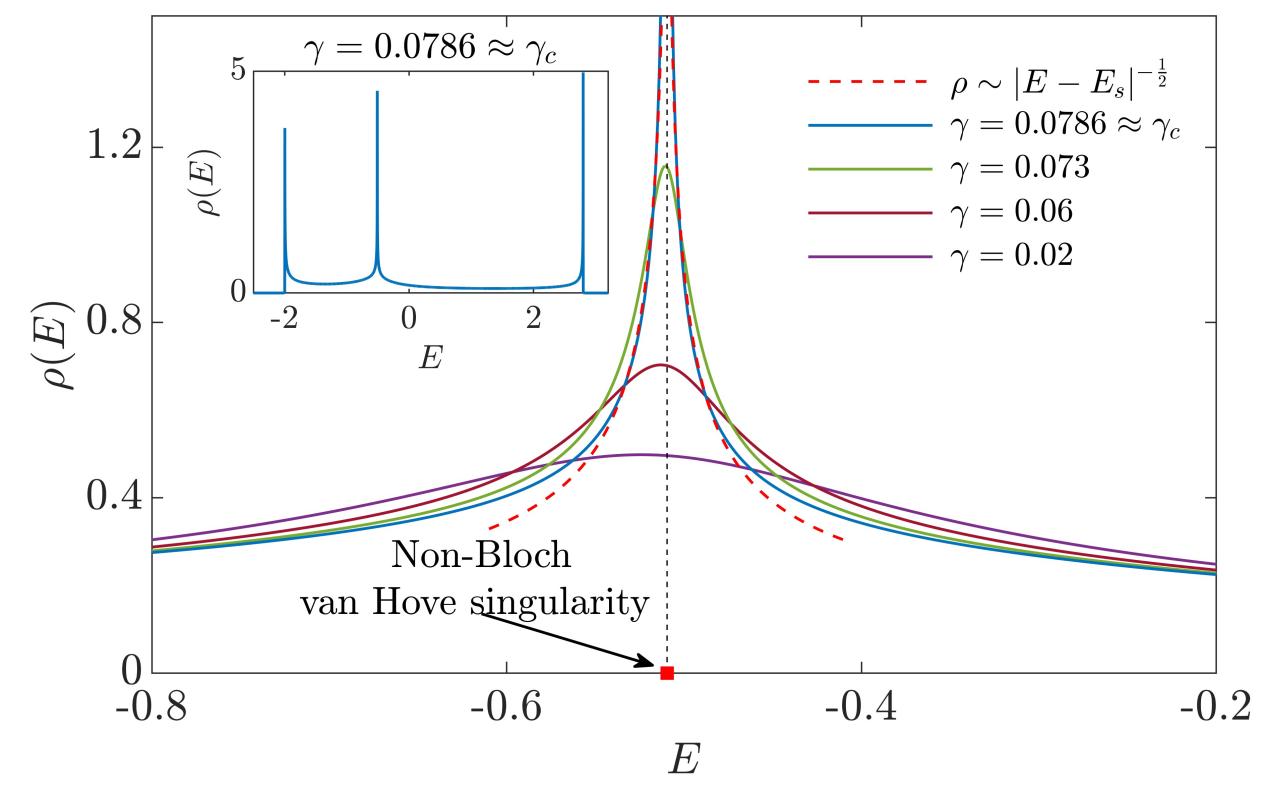
图4：此图展示了当非布洛赫PT对称性尚未破缺时的实数能谱的能态密度。随着非厄米参数增大至PT对称性破缺的临界情况，能态密度在非布洛赫范霍夫奇点处发散。

该研究成果以《Geometric Origin of non-Bloch PT Symmetry Breaking》为题发表于Physical Review Letters. 论文作者为清华大学高等研究院2019级博士生、现德国马克斯-普朗克研究所博士后胡渝民，2021级博士生汪弘毅，2018级博士生、现中国科学院大学卡弗里理论科学研究所博士后宋飞 (通讯作者) 和汪忠教授。此工作得到了国家自然科学基金的支持。

论文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.050402