近期，清华大学高等研究院汪忠教授研究组师生在精确可解的量子多体动力学与量子热化问题方面取得进展。他们提出了非平衡量子多体动力学的一类严格解。

量子多体物理研究的核心问题之一是理解热力学如何从非平衡多体动力学中演生。一种解释认为，量子多体系统可以充当其子系统的热库；在热库的影响下，子系统会表现出热化的现象，趋向热平衡态。这种观点促成了本征态热化假说的建立与发展。然而，由于量子多体系统的复杂性，精确刻画其作为子系统热库的性质仍然是一个巨大的挑战。

一种研究思路是从量子线路 (Quantum circuit) 的可解模型中获得启发。量子线路描述的是在时间和空间上均为离散化的多体动力学【如图1（a）所示】。尽管量子线路是连续时间哈密顿量演化的近似和简化，但是仍保留了大多数量子多体动力学的普遍性质，特别是量子热化。因此，作为研究与模拟量子多体系统的重要平台，量子线路得到了广泛关注。2019年， T. Prosen等人提出了一类可解模型，即时空对偶的量子线路，其中局域的量子门在时间和空间方向上都具有幺正性（dual-unitary）。随后，在2021年，D. Abanin等人将Feynman-Vernon影响泛函引入到量子线路的研究中，发展了影响矩阵(influence matrix)方法。他们由此严格证明，在时空对偶的量子线路中，系统可视为一个无穷高温的热库，对子系统产生完全退相干的作用。然而，时空对偶量子线路的可解性局限于某些特定初态上；同时，其作为无穷高温热库的行为比较特殊。因此，构造更为一般的可解量子线路，对理解量子热化现象具有重要意义。

近期，清华高研院汪忠研究组提出了一种系统性的构造方法，针对任意的矩阵乘积态初态，构造出可解量子线路。研究组通过张量网络与影响矩阵方法严格证明【图1（b, c）】，在这些构造出的量子线路中，系统所充当的热库行为可以由量子通道(quantum channel)描述，其作用的细节由初态完全决定，表现出强烈的非马尔可夫性。更为有趣的是，通过将有限维数的额外自由度与子系统相复合，可以消除非马尔可夫性，表现为复合系统的马尔可夫演化；类比经典的隐马尔可夫过程，他们称这类量子线路具有量子隐马尔可夫动力学 (hidden Markovian dynamics)【图1（d）】。

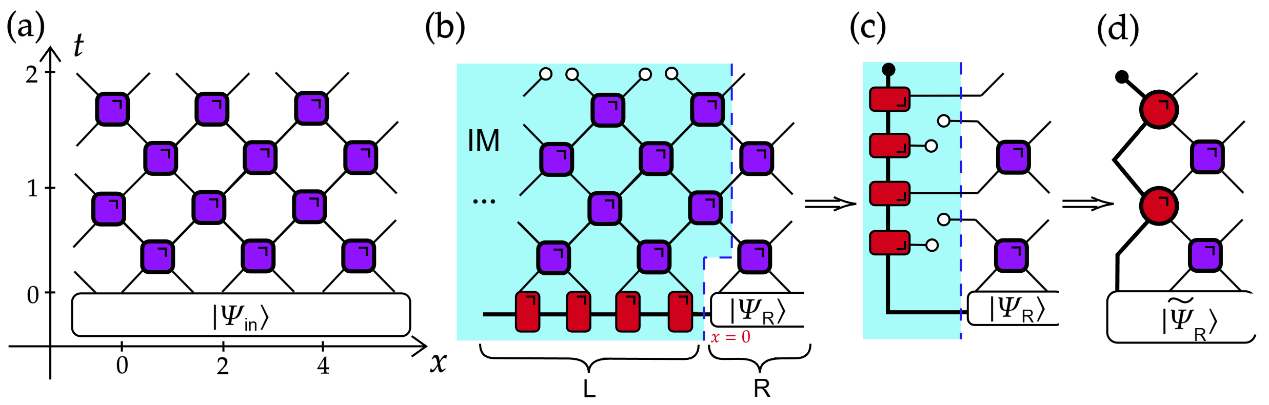
图1：（a）量子线路示意图；（b）矩阵乘积态作为初态与影响矩阵的定义示意图；（c）可解量子线路的影响矩阵；（d）隐马尔可夫动力学。

这项工作构造了一类全新的可解量子线路，其中发展的理论工具可能为未来研究可解量子线路的普遍机制带来启发。文中思路可能有助于进一步理解量子热化现象的微观图像。

该研究成果以《Exact Hidden Markovian Dynamics in Quantum Circuits》为题发表于《Physical Review Letters》。论文的第一作者为清华大学高等研究院2021级博士生王鹤然，第二作者为物理系2021级本科生杨晓旸，通讯作者为汪忠教授。此项目得到了国家自然科学基金与国家重点研发计划的支持。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.170402