流体是自然界中最常见的物态之一。对于流体而言，构成流体的原子、分子之间的相互作用至关重要。比如水，正因为微观上水分子之间推推搡搡，才使得水在宏观上表现出流体的行为。无论是对经典流体还是量子流体，流体力学方程都是描述流体运动的基本手段。

如果有人说，有一类流体力学方程的解，可以用无相互作用自由粒子的运动来构造，你会不会觉得很惊讶？近日，华师大史哲雨研究员、浙师大高超副教授和高研院翟荟教授在Physical Review X上发表的论文“Ideal-Gas Approach to Hydrodynamics”，就是发现了这样一件事情。

事实上，这个想法可以在一些流体的常见现象窥见端倪。比如孤子，可以按照确定的速度运动并保持其形状很长时间，就非常类似于自由粒子的运动。2019年，法兰西公学院Jean Dalibard教授的实验组，在Physical Review X上报道了这样一个实验现象：他们研究了不同初条件下，二维玻色-爱因斯坦凝聚体在谐振子势阱中的运动。他们发现等边三角形的初条件最为特别。只有在这种初条件下，玻色凝聚体在谐振子势阱中振荡，总是可以周期性地、完美地回到初始状态。虽然玻色凝聚体的运动是量子流体的行为，由相互作用主导，但其表现仿佛就是自由粒子在谐振子势阱中的运动。而这一行为只对等边三角形的初态才成立。一时间，这成为一个很难理解的困惑。

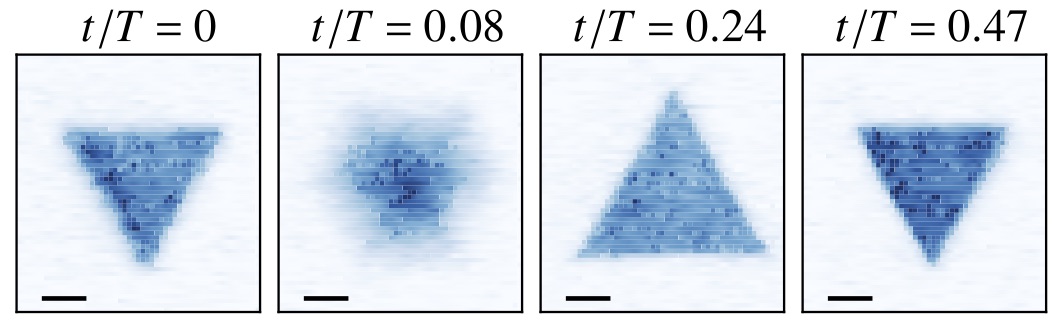
法兰西公学院实验组在Physical Review X上发表的实验结果

(图源自Physical Review X, 9, 021035 (2019))

史哲雨、高超和翟荟致力于解决这个问题。针对这一问题的研究，引导他们发现了一类流体力学方程的严格解，其一般性已经超过了解释这个实验本身，可以在一个统一的框架下理解包括这个实验和孤子在内的多个现象。简单地说，他们考虑无相互作用的玻尔兹曼方程，也可以称为单粒子Liouville方程。这些方程的解是单粒子分布函数，可以直接用自由粒子运动的轨迹得到。他们发现，由这样的分布函数给出的密度场和速度场，可以严格地满足一类流体力学方程的解。这类严格解既包括一维非线性薛定谔方程的孤子解，也包括相互作用满足标度变性时(比如二维玻色凝聚体)一些特殊初条件的解。他们给出了这些特殊初条件所需要满足的几何要求，这就包括了二维情况下的等边三角形和三维情况下的正四面体。

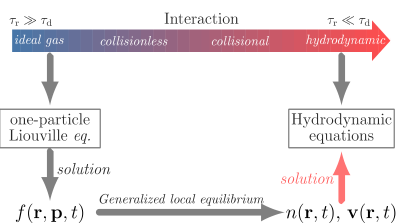
示意图：该工作用自由粒子的运动构造了相互作用流体力学方程的严格解

（图源自Physical Review X, 11, 041031 (2021)）

他们的文章去年在arXiv上贴出以后，很快得到了国际同行的关注。马萨诸塞大学的Olshanii教授，因为其对本征态热化假说(Eigenstate themalization Hypothesis)的研究和在冷原子体系中发现束缚诱导共振(Confinement-induced Resonance)而知名。他和合作者最近就连续发表了两篇文章(arXiv: 2102.12184, arXiv: 2108.09915)，发展了相关研究。文章中称这个严格解为“Shi-Gao-Zhai Solution”,并认为这个工作来源于ingenious insight。文章在Physical Review X审稿过程中，其原创性也获得了两位审稿人一致的高度评价。其中一位审稿人说，这是一篇只需要一个参考文献(即Jean Dalibard的实验)的论文。

由史哲雨、高超和翟荟教授完成的这一工作，被同行称为“Shi-Gao-Zhai Solution”

史哲雨于2011-2016年在高研院读博士，是翟荟教授指导的第二位博士研究生，现为华东师范大学精密光谱科学与技术国家重点实验室研究员。高超于2010-2015在高研院读博士，是翟荟教授指导的第一位博士研究生，现为浙江师范大学副教授。

流体力学方程被广泛地用于物理学的很多分支领域。这类严格解能否在更一般的情况下成立，从而对物理学其他分支产生影响，是未来值得研究的问题。

原文链接：

https://journals.aps.org/prx/abstract/10.1103/PhysRevX.11.041031